対数で小さい数字は表せます。ルールブックが間違い。
TORGの対数は小さい数が表せないことになっていますが、数学的には表せます。
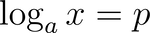
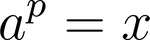
対数表というものがあって、TORGでは表参照すると数値(真数)と基本値(対数)が対応しています。
xが真数、pが対数、aが底です。
普通の運用では
真数(数値)の掛け算は対数(基本値)の足し算になります。
真数(数値)の割り算は対数(基本値)の引き算になります。
真数(数値)と真数(数値)の足し算は真数(数値)と真数(数値)を足し算します。
真数(数値)と真数(数値)の引き算は真数(数値)と真数(数値)を引き算します。
対数表というものがあって、普通の運用では常用対数(底が10)や自然対数(ネイピア数e)を使います。
(PR)丸善対数表 第17版
対数表の使い方でわかりやすいのは
(PR)Newton 対数の威力 Kindle版
小さい数を表すには割り算を考えればいいので、対数(基本値)引く対数(基本値)でOK。
対数(基本値)の割り算掛け算は指数倍のことです。
対数システムはTORGのオリジナルではなく対数表や計算尺に用いられる枯れた技術です。
デザインの意図は対数(基本値)による計算の簡略化のものではないでしょうか。
ルール記述通り、5乗で10倍なら、
LOG(10, 1.584893192)
※LOG(真数,底)
になるとすると、1の増加は、1.584893192倍になります。
1.584893192^5=10
を考えれば良いのです。
1上昇するとほぼ1.5倍という記述もありますが、好意的に解釈するのでしょう。
要するに1.584893192に同じ1.584893192を対数(基本値)回掛けたら真数(数値)になるという事です。
※TORGの底は、10^(1/5)=10^(0.2)ですから1.584893192ともとめられます。
※LOG(10,10^(1/5))は、底の1/5乗を外して底を10として、対数に1/5の逆数(つまり5)を掛ければ同じになります。つまり常用対数表(底が10)の5倍の対数です。
こちらのサイトが分かりやすい。
よくTORGで対数(基本値)に整数を割り算掛け算する人がいますが、それは面積とかエネルギーとか体積(重量)を求めるようなとき(べき乗・累乗する)だけで、基本は掛け算割り算を足し算引き算にするということになります。
例として、
数値が100(基本値10)と数値25(基本値7)なら、
数値の掛け算100×25=2500を、
基本値で考えると10+7=17(数値2500に対応する)
という原理です。
割り算は引き算になりますので、
数値2500(基本値17)割る数値25(基本値7)なら
数値の割り算2500÷25=100は
基本値の引き算17-7=10(基本値10は数値100)です。
ところがTORGはアバウトな丸めた値の参照をするので、つじつまが合わず、理解に苦労します。
あと高校数学で習ったという「たいすうの法則」は対数ではなくて大数なので、大数の法則は習いましたが対数の法則ではありません。一体、何が関係するのかサッパリです。こういうのが混乱の元です。
下の表は微妙な値を計算したものです。小さい数値を扱えないはずはありません。大きい分母の分数とかマイナス乗を考えれば良いだけです。
対数による演算は実用的(手計算)には上三桁くらいの精度です。
対数の底10^0.2での
対数と底10^0.2 の対数乗表 つまり(10^(1/5))^(対数)
| -1 |
0.6309573447 |
| -0.9 |
0.6606934482 |
| -0.8 |
0.6918309711 |
| -0.7 |
0.7244359602 |
| -0.6 |
0.7585775752 |
| -0.5 |
0.7943282348 |
| -0.4 |
0.8317637712 |
| -0.3 |
0.87096359 |
| -0.2 |
0.9120108394 |
| -0.1 |
0.954992586 |
| 0 |
1 |
| 0.1 |
1.047128548 |
| 0.2 |
1.096478196 |
| 0.3 |
1.148153621 |
| 0.4 |
1.202264434 |
| 0.5 |
1.258925412 |
| 0.6 |
1.318256738 |
| 0.7 |
1.380384264 |
| 0.8 |
1.44543977 |
| 0.9 |
1.513561248 |
| 1 |
1.584893192 |
(PR)トーグ リヴァイスド エディション
(PR)コンサイス(Concise) 定規 円形計算尺 300 100829
(PR)APR Student Pilot E6-Bフライトコンピューター トレーニングNP-8プロッタ付き - E6-B8DP
関数電卓 Panecalで計算手順を示し原理を説明します。
消費税の10%を表現したい場合は、十分の十一税ですから、
常用対数の場合、10が底ならば、
log(11)-log(10)
=log(1)
=0.041392685158
ですね。
この0.041392685158はどこかに置いておいて対数だけで計算できます。
10000enのものを買ったら常用対数では4ですから、
log(4)-(log(11)-log(10))
=log(3)
つまりlogを外してしまって
4-(11-10)=3
として
を3を常用対数表を参照するか、常用対数の底10に10^(3)すると、1000enと出ます。
べき乗(つまり累乗)は
E=mc^2 を例にします。
かりにm=10,c=3とします。
まんま計算すると
10×3^(2)=90
ですね。
掛け算を足し算にしてべき乗は掛け算にする。自然対数eが底ならば
ln(10)+2×ln(3)
足し算と掛け算に出来ます。
自然対数のべき乗を求める。
e^(ln(10)+2×ln(3))=89.999
(e^()は自然対数表を参照するという意味です。およそ90)
底が違っても同じ事で、常用対数の場合、10が底ならば
log(10)+2×log(3)
10^(log(10)+2×log(3))=89.999
(10^()は常用対数表を参照するという意味です。およそ90)
この通り底が変わっても計算は成立します。
TORGの底である10^(1/5)つまり1.584893192にしても同様に成立します。
基本値を二倍するというルールの記述は要するに二乗しているということです。何か謎の計算をしているわけではありません。
よく間違われるケースとして、
足し算したい場合、対数だけで
常用対数1と常用対数5を log(1)+log(5)=log(5)
なんて妙なことをやるのは間違いです。
この場合計算間違いになってしまいます。
log(1)=0
log(5)=0.698970004
なので加算すると
log(5) ?
それとも
log(1+5)
=log(6)
掛け算になる?
でしょうか。
いいえ、両方とも間違いです。
真数の足し引き算はせず、logならば、ちゃんと計算します。
底は10なので、真数を求めます。真数は底の対数乗です。
10^1+10^5=10+100000=100010です。
100010の対数は底を10にすれば5.000043です。
確かめるとlog(5)は0.698970004です。log(6)は0.778151250です。
このように計算が合いませんね。
対数を加算・減算するのは掛け算・割り算の時だけです。
加算・減算したいときは対数の真数を求めて真数を加算・減算します。
TORGで言うのなら基本値を足し引き算するのは数値の掛け算割り算を意味しています。
値を足し引き算したい場合は基本値ではなく対応する数値を足し引き算します。
TORGで基本値10と基本値11を加算したい場合は、
底は10^0.2なので、
(10^0.2)^10+(10^0.2)^11
=258.4893192
ここから10^(1/5)つまり、10^0.2を底とした基本値である対数をとると、対数は
LOG((10^0.2)^10+(10^0.2)^11,10^0.2)
=LOG(258.4893192,10^0.2)
=12.06221301
です。
なぜこんなことをしているかと言えば、計算を簡単にするためです。
単なる加算や減算は基本値だけの操作では出来ません。
例えば基本値10と基本値11を掛けたい場合は、本来は掛け算のところを、基本値同士の足し算で10+11=21だけです。基本値21のところにある数値が答えです。掛け算割り算は楽になります。
もしかしたら、TORGのこの常用対数でもなく自然対数でもない底であるといった部分がコズムとかポシビリティとかいったものをデザイン的に表しているのかも知れないと思います。
細かい数値はどうでしょうか。
指数は当たり前ですが大きい数値も細かい数字も表せますね。TORGではなぜか表上にマイナスの対数はありませんが、もちろん表せます。
このマイナスが表にないのと数値の丸めでかえって分かりにくくなっていると思います。
マイナスの対数となるべく丸めない表が下です。
| 対数を底10^0.2で考えた場合 |
| 対数 |
底10^0.2 の対数乗
(真数)
(10^(1/5))^(対数)
()内は丸めた数字と範囲 |
| -20 |
0.0001 |
| -19 |
0.0001584893192 |
| -18 |
0.0002511886432 |
| -17 |
0.0003981071706 |
| -16 |
0.0006309573445 |
| -15 |
0.001 |
| -14 |
0.001584893192 |
| -13 |
0.002511886432 |
| -12 |
0.003981071706 |
| -11 |
0.006309573445 |
| -10 |
0.01 |
| -9 |
0.01584893192 |
| -8 |
0.02511886432 |
| -7 |
0.03981071706 |
| -6 |
0.06309573445 |
| -5 |
0.1 |
| -4 |
0.1584893192 |
| -3 |
0.2511886432 |
| -2 |
0.3981071706 |
| -1 |
0.6309573445 |
| 0 |
1(1) |
| 1 |
1.584893192(2) |
| 2 |
2.511886432(3) |
| 3 |
3.981071706(4~5) |
| 4 |
6.309573445(6~9) |
| 5 |
10(10~14) |
| 6 |
15.84893192(15~24) |
| 7 |
25.11886432(25~39) |
| 8 |
39.81071706(40~59) |
| 9 |
63.09573445(6~99) |
| 10 |
100(100~149) |
| 11 |
158.4893192(150~249) |
| 12 |
251.1886432(250~399) |
| 13 |
398.1071706(400~599) |
| 14 |
630.9573445(600~999) |
| 15 |
1000(1000~1499) |
| 16 |
1584.893192(1500~2499) |
| 17 |
2511.886432(2500~3999) |
| 18 |
3981.071706(4000~5999) |
| 19 |
6309.573445(6000~9999) |
| 20 |
10000(10000~) |
| 21 |
15848.93192(15000~) |
| 22 |
25118.86432(25000~) |
| 23 |
39810.71706(40000~) |
| 24 |
63095.73445(60000~) |
| 25 |
100000(100000~) |
| 26 |
158489.3192(150000~) |
| 27 |
251188.6432(250000~) |
| 28 |
398107.1706(400000~) |
| 29 |
630957.3445(600000~) |
| 30 |
1000000(1000000~) |
| 31 |
1584893.192(1500000~) |
| 32 |
2511886.432(2500000~) |
| 33 |
3981071.706(4000000~) |
| 34 |
6309573.445(6000000~) |
| 35 |
10000000(10000000~) |
| 36 |
15848931.92(15000000~) |
| 37 |
25118864.32(25000000~) |
| 38 |
39810717.06(40000000~) |
| 39 |
63095734.45(60000000~) |
| 40 |
100000000(100000000~) |

