[SYS]最低命中確率

　テ・ア・アゲキャンの本にこんな問題と解がありました。

　空気銃が故障のため暴発したとする。10mの距離のところにある半径10ｃｍの円形目標に命中する確率を求めよ。ただし、弾丸はどこの方向にも等確率で飛んでいくものとする。

　解：弾丸が飛んでいくすべての同様に確からしい方向は無限集合になる。しかし、好都合な場合の数との比は、近似的に

 

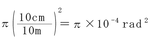
　である目標の立体角と全立体角4π との比に等しい。したがって、求める確率は

 
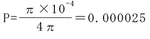
　約0.0025％

　…ずいぶん高い確率です。

　つまり、銃の暴発で10ｍ離れていても、頭を打ち抜かれる確率はこれだけあるということです。